Question

A disk of radius 2.83 m rotates about its axis. Points on the disk's rim undergo tangential acceleration of magnitude 2.53 m/s2. At a particular time the rim has a tangential speed of 1.53 m/s. At a time 0.817 seconds later, what is the tangential speed, v, of a point on the rim, the magnitude of the point's radial acceleration, ar, and the magnitude of its total acceleration, atot?

find:

V=

a(radial)=

a(total)=

Answer 1

(a). The tangential speed is 3.597 m/s.

(b). The magnitude of the point's radial acceleration is 4.57 m/s².

(c). The magnitude of its total acceleration is 5.22 m/s².

Step-by-step explanation:

Given that,

Radius of disk = 2.83 m

Acceleration = 2.53 m/s²

Tangential speed = 1.53 m/s

Time = 0.817 s

(a). We need to calculate the tangential speed

Using equation of motion

`v = u+at`

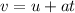
Where, v = final velocity

a = acceleration

T = time

Put the value into the formula

`v=1.53+2.53*0.817`

`v=3.597\ m/s`

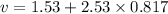
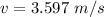
(b). We need to calculate the magnitude of the point's radial acceleration

Using formula of radial acceleration

`a_(r)=(v^2)/(r)`

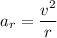
Put the value into the formula

`a_(r)=(3.597^2)/(2.83)`

`a_(r)=4.57\ m/s^2`

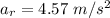
(c). We need to calculate the magnitude of its total acceleration

`a_(tot)=\sqrt{a_(r)^2+a_(t)^2}`

`a_(tot)=√((4.57)^2+(2.53)^2)`

`a_(tot)=5.22\ m/s^2`

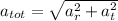
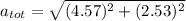
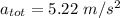
Hence, (a). The tangential speed is 3.597 m/s.

(b). The magnitude of the point's radial acceleration is 4.57 m/s².

(c). The magnitude of its total acceleration is 5.22 m/s².

Answer 2

Step-by-step explanation:

v = u + at

= 1.53 + 2.53 x0.817

= 3.6 m/s

Radial acceleration = v² / r

= 3.6 x 3.6 / 2.83

a_r = 4.58 m / s²

a_tot = √ 4.58² + 2.53²

= √ (20.97 + 6.4)

= 5.23 m /s²