Question

If the probability that a research project will be well planned is 0.8 ; will be well executed is 0.9; and the probability that it will be well planned and well executed is 0.72; a) What is the probability a research project is well planned; or well executed; or well planned and well executed? b) What is the probability a research project is only well planned or well executed but not well planned and well executed : c) What is the probabilit y a research project which is well planned will also be executed? d) What is the probability a research project which is well executed will also be well planned? e) What is the probability a research project is not planned and/or not well executed? f) What is the probability a research project is only well planned? g) What is the probability a research project is only well executed? h ) Are these two events (Well Planned / Well Executed) Mutually Exclusive? i ) Are these two events (Well Planned / Well Executed) Independent? Annotations

Answer 1

Explanation:

Let A = research project will be well planned

B = research project will be well executed

P(A) = 0.8

P(B) = 0.9

P(AB) = 0.72

a) the probability a research project is well planned; or well executed; or well planned and well executed=
`P(AUB) = 0.8+0.9-0.72 =0.98`

(b) the probability a research project is only well planned or well executed but not well planned and well executed :
`=P(AUB) -P(AB) = 0.26`

c) the probabilit y a research project which is well planned will also be executed = P(AB) = 0.72

d) the probability a research project which is well executed will also be well planned = 0.72

e) the probability a research project is not planned and/or not well executed

`= P(A'B') = 1-P(AUB) = 0.02`

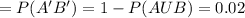
f) the probability a research project is only well planned

`= P(A)-P(AB) = 0.08`

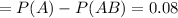
g) the probability a research project is only well executed=P(B) = 0.9

h ) Are these two events (Well Planned / Well Executed) Mutually Exclusive?

No, since P(AB) is not 0

i ) Are these two events (Well Planned / Well Executed) Independent

Yes, since P(AB) = P(A) P(B)