Question

A city has developed a plan to provide for future municipal water needs. The plan proposes an aqueduct that passes through 500 feet of tunnel in a nearby mountain. Two alternatives are being considered. The first proposes to build a full-capacity tunnel now for $556,000. The second proposes to build a half capacity tunnel now (cost = $402,000), which should be adequate for 20 years, and then to build a second parallel half-capacity tunnel. The maintenance cost of the tunnel lining for the full-capacity tunnel is $40,000 every 10 years, and for each half-capacity tunnel it is $32.000 every 10.

The Friction losses in the half-capacity tunnels will be greater than in the full-capacity tunnel. The estimated additional pumping costs in each half-capacity tunnel will be $2000 per year. Based on capitalized cost and a 7% interest rate, which alternative should be selected?

Answer 1

The second alternative capitalized cost is lower thus, it is convient to go for the half-capacity tanks.

Step-by-step explanation:

Full capacity net worth:

556,000 tunnel investment

+ present value of maintenance cost at perpetuity:

`PV / (1-(1+r)^(-time) )/(rate) = C\\`

PV $40,000.00

time 10

rate 0.07

`40000 / (1-(1+0.07)^(-10) )/(0.07) = C\\`

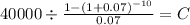
C $ 2,895.100

This will be the annual cost for the maintenance as it is every 10 year we calcualte the perpetuity which gneerates this amount:

$2,895.1 / 0.07 = $41,358.57

Total cost: 556,000 + 41,358.57 = 597,358.57‬

Now, we solve for the cost of the half-capacity. As we already know the value of the first alternative our analisys should stop if we surpass it.

402,000

+ PV of the second

`(Maturity)/((1 + rate)^(time) ) = PV`

Maturity $402,000.0000

time 20.00

rate 0.07

`(402000)/((1 + 0.07)^(20) ) = PV`

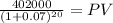
PV 103,884.44

Then, maintencance cost:

`PV / (1-(1+r)^(-time) )/(rate) = C\\`

PV $32,000.00

time 10

rate 0.07

`32000 / (1-(1+0.07)^(-10) )/(0.07) = C\\`

C $ 2,316.080

$33,086.86 for the first one

the second pool will start withdrawals in 20 years so:

`(Maturity)/((1 + rate)^(time) ) = PV`

Maturity $33,086.8600

time 20.00

rate 0.07

`(33086.86)/((1 + 0.07)^(20) ) = PV`

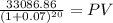
PV 8,550.27

Then, we have a perpetuity of 2,000 dollar for additional pumping cost

on each one:

2,000/0.07 = 28,571.43

the second again is discounted for 20 years:

`(Maturity)/((1 + rate)^(time) ) = PV`

Maturity $28,571.4300

time 20.00

rate 0.07

`(28571.43)/((1 + 0.07)^(20) ) = PV`

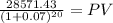
PV 7,383.40

capitalized cost for the second alternative:

402,000 + 103,884.44

+ 33,086.86 + 8,550.27

+ 28,571.45 + 7,383.4

Total capitalized cost: 583,476.42‬