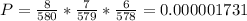Answer:
a. 0.12109
b. 0.0001668
c .0.9726
d. 0.01038
e. 0.01211
f. 0.000001731
Explanation:
Sample size = 580
Defective units = 8
Number of picks = 2
a) If the first container is defective, there 7 defective containers left in a population of 579. The probability of selecting a defective one is:
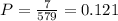
b) The probability that both are defective is given by:

c) The probability that both are acceptable is given by:
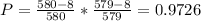
d) In this case, two defective units were removed from the batch, the probability that the third is also defective is:
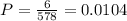
e) In this case, one acceptable and one defective unit were removed from the batch, the probability that the third is also defective is:
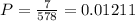
f) The probability that all three are defective is given by: