Answer:
a) For this case we need to find first the degrees of freedom given by:
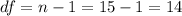
Now we need to find a quantile on the t distribution with 14 degrees of freedom that accumulates 0.05 of the area on the right and 0.95 on the left. And this value is:
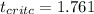
And we can obtained with the following Excel code :"=T.INV(0.95,14)"
So for this case we will reject the null hypothesis if
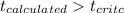 or if
or if
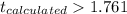
b)
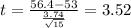
Explanation:
Data given and notation
We have the following dataset:
53 57 50 55 58 54 60 52 59 62 60 60 51 59 56
We can calculate the mean and deviation with the following formulas:
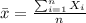
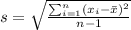
And the results are:
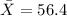 represent the sample mean
represent the sample mean
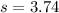 represent the sample standard deviation
represent the sample standard deviation
 sample size
sample size
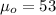 represent the value that we want to test
represent the value that we want to test
 represent the significance level for the hypothesis test.
represent the significance level for the hypothesis test.
t would represent the statistic (variable of interest)
 represent the p value for the test (variable of interest)
represent the p value for the test (variable of interest)
State the null and alternative hypotheses.
We need to conduct a hypothesis in order to check if the mean is higher than 53, the system of hypothesis would be:
Null hypothesis:

Alternative hypothesis:
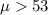
If we analyze the size for the sample is > 30 but we don't know the population deviation so is better apply a t test to compare the actual mean to the reference value, and the statistic is given by:
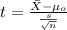 (1)
(1)
t-test: "Is used to compare group means. Is one of the most common tests and is used to determine if the mean is (higher, less or not equal) to an specified value".
a) Decision rule
For this case we need to find first the degrees of freedom given by:
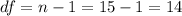
Now we need to find a quantile on the t distribution with 14 degrees of freedom that accumulates 0.05 of the area on the right and 0.95 on the left. And this value is:
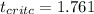
And we can obtained with the following Excel code :"=T.INV(0.95,14)"
So for this case we will reject the null hypothesis if
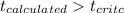 or if
or if
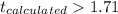
b) Calculate the statistic
We can replace in formula (1) the info given like this:
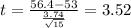
Conclusion
As we can see our calculated value is higher than the critical value 3.52>1.76 so then we are on the rejection zone and we can conclide that that we have enough evidence to reject the null hypothesis, so the means seems to be higher than 53 at 5% of signficance.