Answer:
Step-by-step explanation:
given,
Mean,μ= 35mm
Standard Deviation,σ = 0.5mm
Sample size, n = 36
Sample Standard deviation =
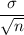
=
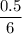
= 0.0833
The interested diameter is between 34.95 to 35.18 mm
Calculating the Z score of the for the diameter mentioned.
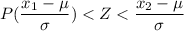
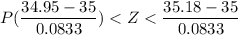
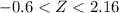
now, Form Z-table
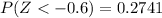
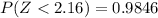
Subtracting the value
= 0.9846 - 0.2741
= 0.71
Hence, the required probability is that the diameter of bearing is in between 34.95 and 35.18 mm is equal to 0.71.