Question

At 293 K, methanol has a vapor pressure of 97.7 Torr and ethanol has a vapor pressure of 44.6 Torr. What would be the vapor pressure of a mixture of 80 g of ethanol and 97 g of methanol at 293 K?

Answer 1

Answer: The vapor pressure of a mixture of 80 g of ethanol and 97 g of methanol at 293 K is 78.3 torr.

Step-by-step explanation:

According to Raoult's law, the vapor pressure of a component at a given temperature is equal to the mole fraction of that component multiplied by the vapor pressure of that component in the pure state.

`p_1=x_1p_1^0` and
`p_2=x_2P_2^0`

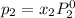
where, x = mole fraction in solution

`p^0` = pressure in the pure state

According to Dalton's law, the total pressure is the sum of individual pressures.

`p_(total)=p_1+p_2`
`p_(total)=x_Ap_A^0+x_BP_B^0`

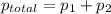
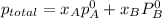
moles of ethanol=
`\frac{\text{Given mass}}{\text {Molar mass}}=(80g)/(46g/mol)=1.7moles`

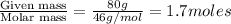
moles of methanol=
`\frac{\text{Given mass}}{\text {Molar mass}}=(97g)/(32g/mol)=3.0moles`

Total moles = moles of ethanol + moles of methanol = 1.7 +3.0 = 4.7

`x_(ethanol)=(1.7)/(4.7)=0.36,`

`x_(methanol)=1-x_(ethanol)=1-0.36=0.64`

`p_(ethanol)^0=44.6torr`

`p_(methanol)^0=97.7torr`

`p_(total)=0.36* 44.6+0.64* 97.7=78.3torr`

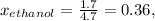
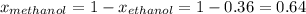
Thus the vapor pressure of a mixture of 80 g of ethanol and 97 g of methanol at 293 K is 78.3 torr.