Question

An archer releases an arrow with an initial velocity of 20 feet per second at a height of 12 feet. The path the arrow takes can be modeled using the function f(x)=−16x^2+20x+12, where f(x) represents the height, in feet, of the arrow and x represents the time the arrow travels in seconds. What is the maximum height, in feet, reached by the arrow? Round your answer to the nearest hundredth if necessary. Do not include units in your answer.

Answer 1

18.25

Explanation:

we are given a quadratic function

`f(x) = - 16 {x}^(2) + 20x + 12`

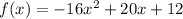
where:

• f(x) represents the height
• x represents the time

To find the maximum value of f(x) in other words, the maximum height, in feet, reached by the arrow.

Differentiate both sides:

`f'(x) = (d)/(dx)( - 16 {x}^(2) + 20x + 12)`

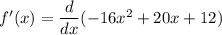
with sum differentiation rule, we acquire:

`\displaystyle f'(x) = (d)/(dx)( - 16 {x}^(2) )+ (d)/(dx) 20x + (d)/(dx) 12`

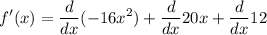
recall that,

• differentiation of a constant is equal to 0
• 
  `(d)/(dx) {x}^(n) = n {x}^(n - 1)`

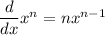
utilizing the rules we acquire:

`\displaystyle f'(x) = - 32 {x}^{} + 20`

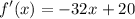
now equate f'(x) to 0:

`\displaystyle - 32 {x}^{} + 20 = 0`

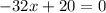
solving the equation for x yields:

`x _(max)= (5)/(8)`

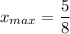
plug in the maximum value of x into the quadratic function:

`f(x )_(max)= - 16 {( (5)/(8) )}^(2) + 20( (5)/(8) ) + 12`

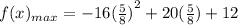
simplify:

`f(x )_(max) = 18.25`

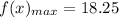
hence,

The maximum height reached by the arrow is 18.25 feet

Answer 2

• 18.25 feet

Explanation:

The given function is quadratic.

The maximum of the quadratic function is its vertex.

The x-coordinate is determined by x = - b/(2a)

• x = - 20/(-16*2) = 5/8

Apply the x-value and find the value of f:

• f(x) = - 16(5/8)² + 20(5/8) + 12 = 18.25 feet