Question

A large well-mixed tank of unknown volume, open to the atmosphere initially, contains pure water. The initial height of the solution in the tank is unknown. At the start of the experiment a potassium chloride solution in water starts flowing into the tank from two separate inlets. The first inlet has a diameter of 1 cm and delivers a solution with a specific gravity of 1.07 and a velocity of 0.2 m/s. The second inlet with a diameter of 2 cm delivers a solution with a velocity of 0.01 m/s and a density of 1053 kg/m3. The single outflow from this tank has a diameter of 3cm. A colleague helps you by taking samples of the tank and outflow in your absence. He samples the tank and determines that the tank contains 19.7 kg of potassium chloride. At the same moment he measures the flow rate at the outlet to be 0.5 L/s, and the concentration of potassium chloride to be 13 g/L. Show that your colleague took the samples after 25 minutes. The tank and all the inlet solutions are maintained at a constant temperature of 80 °C. Calculate the exact time when the sample were taken.

Answer 1

The exact time when the sample was taken is = 0.4167337 hr

Step-by-step explanation:

The diagram of a sketch of the tank is shown on the first uploaded image

Let A denote the first inlet

Let B denote the second inlet

Let C denote the single outflow from the tank

From the question we are given that the diameter of A is = 1 cm = 0.01 m

Area of A is =
`(\pi)/(4)(0.01)^(2) m^(2)`

=
`7.85 *10^(-5)m^(2)`

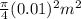
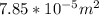
Velocity of liquid through A = 0.2 m/s

The rate at which the liquid would flow through the first inlet in terms of volume =
`(Volume of Inlet )/(time)` =
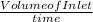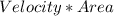`Velocity * Area` i.e is
`m^(2) * (m)/(s) = (m^(3))/(s)`

=
`0.2 *7.85*10^(-5) (m^(3))/(s)`

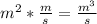
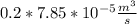
The rate at which the liquid would flow through the first inlet in terms of mass of the liquid = mass of liquid × the rate of flow in terms of volume

=
`1039.8 * 0.2 * 7.85 *10^(-5) Kg/s`

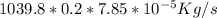
= 0.016324
`(Kg)/(s)`

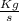
From the question the diameter of B = 2 cm = 0.02 m

Area of B =
`(\pi)/(4) * (0.02)^(2) m^(2) = 3.14 * 10^(-4)m^(2)`

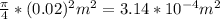
Velocity of liquid through B = 0.01 m/s

The rate at which the liquid would flow through the first inlet in terms of volume =
`(Volume of Inlet )/(time)` =
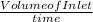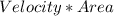`Velocity * Area` i.e is
`m^(2) * (m)/(s) = (m^(3))/(s)`

=
`3.14*10^(-4) *0.01 (m^(3))/(s)`

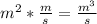
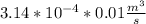
The rate at which the liquid would flow through the second inlet in terms of mass of the liquid = mass of liquid × the rate of flow in terms of volume

=
`1053 * 3.14*10^(-6) (Kg)/(s)`

= 0.00330642
`(Kg)/(s)`

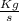
From the question The flow rate in term of volume of the outflow at the time of measurement is given as = 0.5 L/s

And also from the question the mass of potassium chloride at the time of measurement is given as 13 g/L

So The rate at which the liquid would flow through the outflow in terms of mass of the liquid = mass of liquid × the rate of flow in terms of volume

=
`13(g)/(L) * 0.5 (L)/(s)`

=
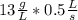
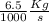`(6.5)/(1000)(Kg)/(s)` Note (1 Kg = 1000 g)

= 0.0065 kg/s

Considering potassium chloride

Let denote the rate at which liquid flows in terms of mass as as
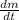`(dm)/(dt)` i.e change in mass with respect to time hence

Input(in terms of mass flow ) - output(in terms of mass flow ) = Accumulation in the Tank(in terms of mass flow )

(0.016324 + 0.00330642) - 0.0065 =
`(dm)/(dt)`

`\int\limits {(dm)/(dt) } \, dx =\int\limits {0.01313122} \, dx`

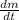
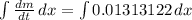
=> 0.01313122 t = (m -
`m_(o)`)

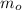From the question (m -
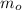`m_(o)`) is given as = 19.7 Kg

Hence the time when the sample was taken is given as

0.01313122 t = 19.7 Kg

=> t = 1500.2414 sec

t = .4167337 hours (1 hour = 3600 seconds)