Answer
given,
Speed of vehicle = 65 mi/hr
= 65 x 1.4667 = 95.33 ft/s
e = 0.07 ft/ft
f is the lateral friction, f = 0.11
central angle,Δ = 38°
The PI station is
PI = 250 + 50
= 25050 ft
using super elevation formula

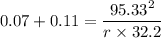
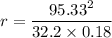
r = 1568 ft
As the road is two lane with width 12 ft
R = 1568 + 12/2
R = 1574 ft
Length of the curve


L = 1044 ft
Tangent of the curve calculation

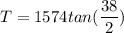
T = 542 ft
The station PC and PT are
PC = PI - T
PC = 25050 - 542
= 24508 ft
= 245 + 8 ft
PT = PC + L
= 24508 + 1044
=25552
= 255 + 52 ft
the middle ordinate calculation
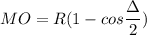
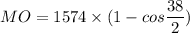
MO = 85.75 ft
degree of the curvature
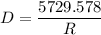
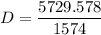
D = 3.64°