Answer:
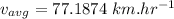
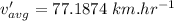

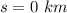 because the person finally return to the initial position.
because the person finally return to the initial position.
Step-by-step explanation:
Given:
velocity during the first half,
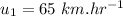
velocity during the second half,

velocity during the first half of onward journey,
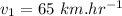
velocity during the second half of onward journey,
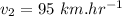
Let the total displacement and distance between the two points be 2x meters.
So, the time taken for the first half of the journey:
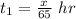
The time taken for the second half of the journey:
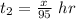
Time taken for the first half of onward journey:
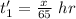
Time taken for the first half of onward journey:

average speed going down to St. Louis:

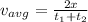
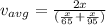
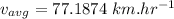
Similarly, average speed coming back from St. Louis:
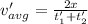
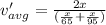
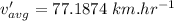
Now the total average speed of the trip:
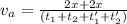
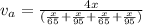

Total displacement during the entire trip:
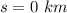 because the person finally return to the initial position.
because the person finally return to the initial position.