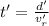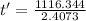Answer:
1)
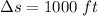
2)
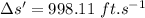
3)
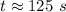

Step-by-step explanation:
Given:
width of river,

speed of stream with respect to the ground,
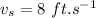
speed of the swimmer with respect to water,
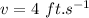
Now the resultant of the two velocities perpendicular to each other:

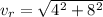
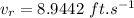
Now the angle of the resultant velocity form the vertical:
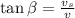
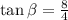
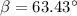
- Now the distance swam by the swimmer in this direction be d.
so,
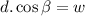

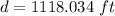
Now the distance swept downward:
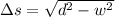
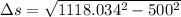
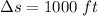
2)
On swimming 37° upstream:
The velocity component of stream cancelled by the swimmer:
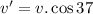

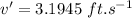
Now the net effective speed of stream sweeping the swimmer:
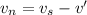

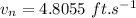
The component of swimmer's velocity heading directly towards the opposite bank:
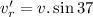

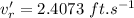
Now the angle of the resultant velocity of the swimmer from the normal to the stream:
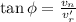
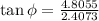
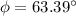
- Now let the distance swam in this direction be d'.
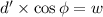


Now the distance swept downstream:
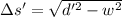
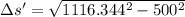
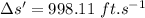
3)
Time taken in crossing the rive in case 1:
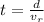
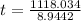
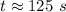
Time taken in crossing the rive in case 2: