To prove the QRST is a parallelogram.
Step 1: Given
 and
and
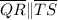
Step 2:
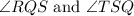 are alternate interior angles.
are alternate interior angles.
Definition of alternate interior angles
Step 3: Alternate interior angle theorem:
If two parallel lines cut by a transversal then the alternate interior angles are congruence.
QR and TS are parallel lines cut by QS.
Therefore,
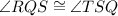
Step 4: Reflexive property of congruence:
Any geometric figure is congruence to itself.
Therefore,
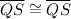
Step 5: By the above steps
 (Angle),
(Angle),
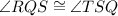 (Angle) and
(Angle) and
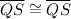 (Side)
(Side)
Hence
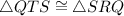 (by ASA congruence theorem)
(by ASA congruence theorem)
Step 6: Corresponding parts of congruence triangles are congruent.
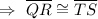
Step 7: Property of parallelogram:
If one pair of opposite sides are both parallel and congruent, then the quadrilateral is a parallelogram.
Hence Quadrilateral QRST is a parallelogram.