Question

A rectangular field with one side along a river is to be fenced. Suppose that no fence is needed along the river, the fence on the side opposite the river costs $20 per foot, and the fence on the other sides costs $5 per foot. If the field must contain 80,000 square feet, what dimensions will minimize costs?

a) Side Parallel to the River___________ft
b) Each of the other sides _____________ft

Answer 1

a) Side Parallel to the river: 200 ft

b) Each of the other sides: 400 ft

Explanation:

Let L represent side parallel to the river and W represent width of fence.

The required fencing (F) would be
`F=L+2W`.

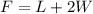We have been given that field must contain 80,000 square feet. This means area of field must be equal to 80,000.

`LW=80,000...(1)`

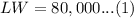
We are told that the fence on the side opposite the river costs $20 per foot, and the fence on the other sides costs $5 per foot, so total cost (C) of fencing would be
`C=20L+5(2W)\Rightarrow 20L+10W`.

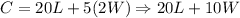From equation (1), we will get:

`L=(80,000)/(W)`

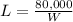
Upon substituting this value in cost equation, we will get:

`C=20((80,000)/(W))+10W`

`C=(1600,000)/(W)+10W`

`C=1600,000W^(-1)+10W`

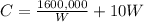
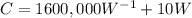
To minimize the cost, we need to find critical points of the the derivative of cost function as:

`C'=-1600,000W^(-2)+10`

`-1600,000W^(-2)+10=0`

`-1600,000W^(-2)=-10`

`-(1600,000)/(W^2)=-10`

`-10W^2=-1,600,000`

`W^2=160,000`

`√(W^2)=\pm√(160,000)`

`W=\pm 400`

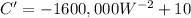
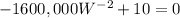
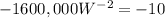
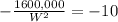
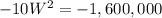
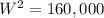
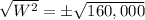
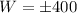
Since width cannot be negative, therefore, the width of the fencing would be 400 feet.

Now, we will find the 2nd derivative as:

`C''=-2(-1600,000)W^(-3)`

`C''=3200,000W^(-3)`

`C''=(3200,000)/(W^3)`

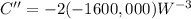
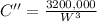
Now, we will substitute
`W=400` in 2nd derivative as:

`C''(400)=(3200,000)/(400^3)=(3200,000)/(64000000)=0.05`

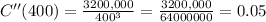
Since 2nd derivative is positive at
`W=400`, therefore, width of 400 ft of the fencing will minimize the cost.

Upon substituting
`W=400` in
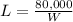`L=(80,000)/(W)`, we will get:

`L=(80,000)/(400)\\\\L=200`

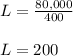
Therefore, the side parallel to the river will be 200 feet.