Question

Directions: Calculate the area of a circle using 3.14x the radius

1) d = 4.4 mm.
Calculate the area of the circle.

2) d = 3.7 cm.
Calculate the area of the circle.

3) r= 8.3 cm.
Calculate the area of the circle.

4) d = 5.8 yd.
Calculate the area of the circle.


5) d = 1 yd.
Calculate the area of the circle

6) r = 8 ft.
Calculate the area of the circle

Answer 1

`\qquad\qquad\huge\underline{{\sf Answer}}♨`

As we know ~

Area of the circle is :

`\qquad \sf  \dashrightarrow \:\pi {r}^(2)`

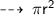
And radius (r) = diameter (d) ÷ 2

[ radius of the circle = half the measure of diameter ]

➖➖➖➖➖➖➖➖➖➖➖➖➖➖➖➖➖

Problem 1

`\qquad \sf  \dashrightarrow \:r = d / 2`

`\qquad \sf  \dashrightarrow \:r = 4.4/ 2`

`\qquad \sf  \dashrightarrow \:r = 2.2 \: mm`

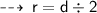
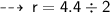
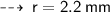
Now find the Area ~

`\qquad \sf  \dashrightarrow \: \pi {r}^(2)`

`\qquad \sf  \dashrightarrow \:3.14 * {(2.2)}^(2)`

`\qquad \sf  \dashrightarrow \:3.14 * {4.84}^{}`

`\qquad \sf  \dashrightarrow \:area \approx 15.2 \: \: mm {}^(2)`

・ ．━━━━━━━†━━━━━━━━━．・

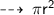
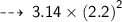
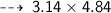
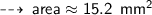
problem 2

`\qquad \sf  \dashrightarrow \:r = d / 2`

`\qquad \sf  \dashrightarrow \:r = 3.7 / 2`

`\qquad \sf  \dashrightarrow \:r = 1.85 \: \: cm`

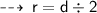
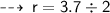
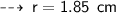
Bow, calculate the Area ~

`\qquad \sf  \dashrightarrow \: \pi {r}^(2)`

`\qquad \sf  \dashrightarrow \:3.14 * (1.85) {}^(2)`

`\qquad \sf  \dashrightarrow \:3.14 * 3.4225 {}^{}`

`\qquad \sf  \dashrightarrow \:area \approx 10.75 \: \: cm {}^(2)`

・ ．━━━━━━━†━━━━━━━━━．・

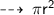
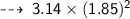
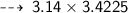
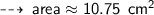
Problem 3

`\qquad \sf  \dashrightarrow \:\pi {r}^(2)`

`\qquad \sf  \dashrightarrow \:3.14 * (8.3) {}^(2)`

`\qquad \sf  \dashrightarrow \:3.14 * 68.89`

`\qquad \sf  \dashrightarrow \:area \approx216.31 \: \: cm {}^(2)`

・ ．━━━━━━━†━━━━━━━━━．・

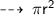
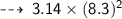
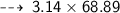
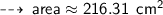
Problem 4

`\qquad \sf  \dashrightarrow \:r = d / 2`

`\qquad \sf  \dashrightarrow \:r = 5.8 / 2`

`\qquad \sf  \dashrightarrow \:r = 2.9 \: \: yd`

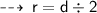
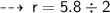
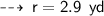
now, let's calculate area ~

`\qquad \sf  \dashrightarrow \:3.14 * {(2.9)}^(2)`

`\qquad \sf  \dashrightarrow \:3.14 * 8.41`

`\qquad \sf  \dashrightarrow \:area \approx26.41 \: \: yd {}^(2)`

・ ．━━━━━━━†━━━━━━━━━．・

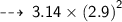
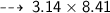
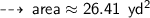
problem 5

`\qquad \sf  \dashrightarrow \:r = d / 2`

`\qquad \sf  \dashrightarrow \:r = 1 / 2`

`\qquad \sf  \dashrightarrow \:r = 0.5 \: \: yd`

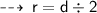
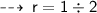
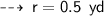
Now, let's calculate area ~

`\qquad \sf  \dashrightarrow \:\pi {r}^(2)`

`\qquad \sf  \dashrightarrow \:3.14 * (0.5) {}^(2)`

`\qquad \sf  \dashrightarrow \:3.14 * 0.25`

`\qquad \sf  \dashrightarrow \:area \approx0.785 \: \: yd {}^(2)`

・ ．━━━━━━━†━━━━━━━━━．・

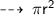
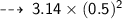
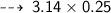
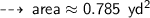
problem 6

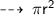
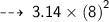
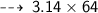
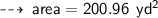
`\qquad \sf  \dashrightarrow \:\pi {r}^(2)`

`\qquad \sf  \dashrightarrow \:3.14 * {(8)}^(2)`

`\qquad \sf  \dashrightarrow \:3.14 * 64`

`\qquad \sf  \dashrightarrow \:area = 200.96 \: \: yd {}^(2)`

➖➖➖➖➖➖➖➖➖➖➖➖➖➖➖➖➖