Question

Rational Area and Irrational Perimeter Question for a Rhombus

Look at Picture

Answer 1

Option d: a rhombus with a side length
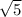`√(5)` units and diagonals with lengths
`√(2)` units and
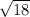`√(18)` units

Step-by-step explanation:

The formula to find the area of the rhombus is
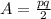`A=(p q)/(2)` where p,q are diagonals.

The formula to find the perimeter of the rhombus is
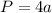`P=4 a` where a is the side length.

Now, we shall determine the rhombus which have a rational area and an irrational perimeter.

Option a: a rhombus with a side length 5 units and diagonals with lengths 8 units and 6 units

Area =
`(8 * 6)/(2)=(48)/(2)=24`

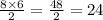
Perimeter =
`4(5)=20`

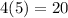
This is a rhombus with a rational area and a rational perimeter.

Hence, Option a is not the correct answer.

Option b: a rhombus with a side length
`√(3)` units and diagonals with lengths
`√(3)` units and
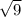`√(9)` units

Area =
`(√(3) * √(9))/(2)=2.59807 \ldots \ldots`

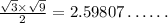
Perimeter =
`4(√(3) )=6.92820......`

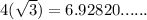
This is a rhombus with irrational area and irrational perimeter.

Hence, Option b is not the correct answer.

Option c: a rhombus with a side length
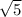`√(5)` units and diagonals with lengths
`√(2)` units and
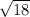`√(18)` units

Area =
`(√(2) * √(18))/(2)=(√(36))/(2)=3`

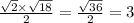
Perimeter =
`4(√(5) )=8.94427......`

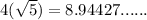
This is a rhombus with rational area and irrational perimeter.

Hence, Option c is the correct answer.

Option d: a rhombus with a side length 2.5 units and diagonals with lengths
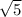`√(5)` units and
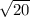`√(20)` units

Area =
`(√(5) * √(25))/(2)=5.59016 \ldots \ldots`

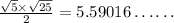
Perimeter =
`4(2.5)=10`

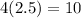
This is a rhombus with an irrational area and a rational perimeter.

Hence, Option d is not the correct answer.