Question

An object with mass 0.240 kg kg is acted on by an elastic restoring force with force constant 10.8 N/m. The object is set into oscillation with an initial potential energy of 0.140 JJ and an initial kinetic energy of 6.50×10^−2 J.

a. What is the amplitude of oscillation?
b. What is the potential energy when the displacement is one-half the amplitude?
c. At what displacement are the kinetic and potential energies equal?
d. What is the value of the phase angle φ if the initial velocity is positive and the initial displacement is negative?

Answer 1

(a) A = 0.194 m.

(b) U = 0.0512 J.

(c) x = 0.137 m.

(d) ∅ = 214°

Step-by-step explanation:

(a) The total energy of the system is the sum of the potential and kinetic energies initially. So,

`E = K_1 + U_1 = 0.140 + 6.5* 10^(-2) = 0.205~J`

According to the initial potential energy, the initial position of the object can be found using the restoring force.

`U_1 = (1)/(2)kx_1^2 = (1)/(2)(10.8)x_1^2 = 0.140\\x_1 = -0.161~m`

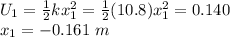
The initial position is negative according to part (d). However, this is not the amplitude of the motion. Since there is an initial kinetic energy, the maximum distance that the object can reach is a little bit further than 0.161 m. Calculating the amplitude taking the initial kinetic energy into account yields

`U = (1)/(2)(10.8)A^2 = 0.205\\A = 0.194~m`

(b) When the displacement is one-half the amplitude, the potential energy becomes

`U = (1)/(2)(10.8)(0.194/2)^2 = 0.0512~J`

(c) For the displacement where the kinetic energy is equal the potential energy, the following equality can be used

`U = K = (E)/(2) = 0.205/2 = 0.1025 ~J\\0.1025 = (1)/(2)kx^2 = (1)/(2)(10.8)x^2\\x = 0.137~m`

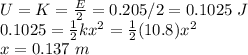
(d) The equation of motion in periodic motion is

`x(t) = A\cos(\omega t + \phi)`

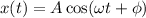
where ∅ is the phase angle.

Initially, t = 0, so the equation of motion becomes

`x(0) = A\cos(\phi) = (0.194)\cos(\phi) < 0`

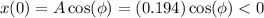
The velocity function is equal to the derivative of the position function with respect to time, and can be written as follows

`v(t) = (dx(t))/(dt) = -\omega A\sin(\omega t + \phi)\\v(0) = -\omega A \sin(\phi) > 0`

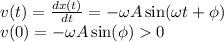
In simple harmonic motion, the angular frequency can be found using the following formula

`\omega = \sqrt{(k)/(m)} = \sqrt{(10.8)/(0.24)} = 6.7~{\rm rad/s}`

In part (a) we have calculated the initial position of the object as -0.161 m.

Therefore,

`-0.161 = (0.194)\cos(\phi)\\\cos(\phi) = -0.83\\\phi = 146^\circ~{\rm or~} 214^\circ`

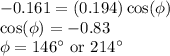
We should check whether this angle is suitable for the velocity function.

The initial velocity can be calculated using the initial kinetic energy.

`K_1 = (1)/(2)mv_1^2 = 6.5* 10^(-2)\\v_1 = 0.73~{\rm m/s}`

Therefore, the velocity function becomes

`0.73 = -(6.7)(0.194)\sin(\phi)\\\sin(\phi) = -0.5616\\\phi = -34^\circ~{\rm or~} 214^\circ`

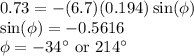
The only angle that can satisfy both conditions is 214°.