Question

For the following exercises, convert the parametric equations of a curve into a rectangular form. No sketch is necessary. State the domain of the rectangular form.

x=t2+2t,y=t+1

Answer 1

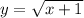`y = √(x+1)` :equation in rectangular form

the domain of the equation is:
`x\geq-1`

Explanation:

We're given two equations:

`x = t^2 + 2t\\y = t+1`

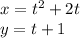
To convert it to rectangular form, we need to get rid of t so that the curve is represented by one equation in terms of only 'x' and 'y'

hence we'll solve both equation simultaneously and eliminate t. Starting from the equation of 'y'

`y = t+ 1\\t=y-1 \rightarrow \text{substitute to equation of $x$}`

`x = t^2 + 2t\\x = (y-1)^2+2(y-1)\\x = y^2-2y+1+2y-2\\x = y^2-1\\y = \pm√(x+1)`

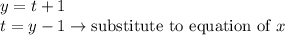
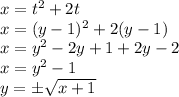
This is the equation of the curve!

The domain of the equation roughly means: what values of x are allowed to be used in the equation. This is important in our case since the square root cannot process negative values. Hence, the values inside the square root MUST be atleast 0 or greater than 0.

that means:

`x+1\geq 0\\x\geq-1`

Hence the domain of the equation is:
`x\geq-1`