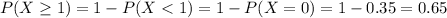Answer:
a)
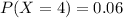
b)
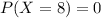
c)
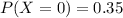
d)
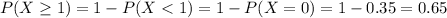
Explanation:
For this case we define the random variable X as "number of books purchased per hit."
And as we can see the distribution for x is given by:
X 0 1 2 3 4 5 6 7
P(X) .35 .25 .20 .08 .06 .03 .02 .01
Part a
For this case we want this probability:
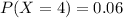 from the probability distribution given
from the probability distribution given
Part b
For this case we want this probability:
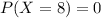 from the probability distribution given since the value of X=8 is not in the distribution
from the probability distribution given since the value of X=8 is not in the distribution
Part c
For this case we want this probability:
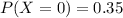 from the probability distribution given
from the probability distribution given
Part d
For this case we want this probability:
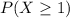
And we can use the complement rule like this: