Question

On Novermber 27, 1993, the New York times reported that wildlife biologists have found a direct ink between the increase in the human population in florida and the decline of the local black bear population. From 1953 to 1993 the human population increased, on average, at a rate of 8% per year, while the black bear population decreased at a rate of 6% per year. In 1853 the black bear population was 11,000.

a) The 1993 human population of Florida was 13 million. What as the human population in 1953?
b) Find the black bear population for 1993.
c) If this trend continues, when will the black bear population number less than 100?

Answer 1

a. 1 263 888

b. 130 701

c. 72 years

Explanation:

a. The differential equation applies here.

Let the quantity increase for a certain time be given by Q(t)

Every unity of time, the quantity increases by
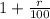`1+(r)/(100)` so that after the time t, the quantity remaining will be given by:

`Q(t) = (1+ (r)/(100) )^(t)`

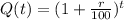
In a similar manner, the quantity R(t) decreases at a rate given by the following expression:

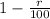`1-(r)/(100)` and after the time , t the quantity of R remaining will be given by:

`R(t) = (1-(r)/(100) )^(t)`

a. To find the population of humans in 1953

`Q(t) = (1+ (r)/(100) )^(t)`

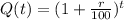
1993 - 1953 = 40 years = t

Q(40) = Q×
`1.06^(40)`

Q = 1 263 888.44

≈ 1 263 888

b. For bear population in 1993:

`R(t) = (1-(r)/(100) )^(t)`

t = 40

R(40) =
`b 0.94^(40) = 11 000`

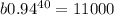
b = 130 700. 889

≈130 701

c. time taken for black bear population number less than 100 is given by:

130 = 11000×
`0.94^(t)`

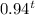
solving using natural logarithms gives t = 72.72666

= 72 years Ans