Question

An advertising agency notices that approximately 1 in 50 potential buyers of a product sees a given magazine ad, and 1 in 5 sees a corresponding ad on television. One in 100 sees both. One in 3 actually purchases the product after seeing the ad, 1 in 10 without seeing it. What is the probability that a randomly selected potential customer will purchase the product?

Answer 1

0.148993

Step-by-step explanation:

Given parameters:

An advertising agency notices that approximately 1 in 50 potential buyers of a product sees a given magazine ad

Let the Probability that the agency notice the buyer of a product sees a given magazine ad be: P (G)

P (G) = 1 in 50

=
`(1)/(50)`

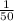
= 0.02

P (G) = 0.02

From the question, it continues by saying " and 1 in 5 sees a corresponding ad on television."

i.e Let the Probability that the agency notice the buyer of a product see the given ad on televison be: P(H)

P(H) = 1 in 5

=
`(1)/(5)`

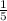
= 0.2

P(H) = 0.2

Let P(I) represent "One in 3 actually purchases the product after seeing the ad"

P(I) =
`(1)/(3)`

P(I) = 0.3333

Let P(J) represent the potential buyer that purchase the product without seeing the ad which is "1 in 10 without seeing it"

P(J) =
`(1)/(10)`

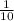
P(J) = 0.1

We are asked to find, the probability that a randomly selected potential customer will purchase the product?

To to that we need to determine first, the probability that the buyer sees the ad of the product both on television and on magazine; as well as the probability that the buyer does not see the ad of the product both on television and on magazine.

Let's take it one after the other;

the probability that the buyer sees the ad of the product both on television and on magazine =

P ( GUH)

Using addition rule;

P ( GUH) = P(G) + P(H) - P(G∩H)

P ( GUH) = 0.02 + 0.2 - 0.01

P ( GUH) = 0.21

the probability that the buyer does not see the ad of the product both on television and on magazine =

P ( GUH)' = 1 - P(GUH) ------ By applying DeMorgan's Rule

P ( GUH)' = 1 - 0.21

P ( GUH)' = 0.79

∴ the probability that a randomly selected potential customer will purchase the product = P(I) P(GUH) + P(J) P(GUH)'

= (0.3333)(0.21) + (0.1) (0.79)

= 0.069993 + 0.079

= 0.148993

Hence, the probability that a randomly selected potential customer will purchase the product = 0.148993