Question

In a local bar, a customer slides an empty beer mug down the counter for a refill. The height of the counter is 1.46 m. The mug slides off the counter and strikes the floor 0.80 m from the base of the counter. (a) With what velocity did the mug leave the counter? Does the time required for the mug to hit the floor depend on its initial horizontal velocity? m/s (b) What was the direction of the mug's velocity just before it hit the floor? ° (below the horizontal)

Answer 1

(a). The horizontal velocity is 1.46 m/s.

(b). The direction of the mug's velocity just before it hit the floor is 74.7° below the horizontal.

Step-by-step explanation:

Given that,

Height of the counter = 1.46 m

Distance = 0.80 m

We need to calculate the time

Using equation of motion

`s_(y)=ut+(1)/(2)gt^2`

`s_(y)=(1)/(2)gt^2`

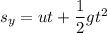
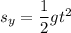
Put the value into the formula

`1.46=(1)/(2)*9.8* t^2`

`t^2=(1.46* 2)/(9.8)`

`t=\sqrt{(1.46*2)/(9.8)}`

`t=0.545\ sec`

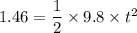
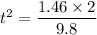
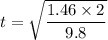
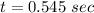
Here, horizontal velocity is constant

(a). We need to calculate the velocity

Using formula of velocity

`v_(x)=(d)/(t)`

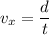
Put the value into the formula

`v_(x)=(0.80)/(0.545)`

`v_(x)=1.46\ m/s`

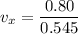
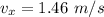
(b). We need to calculate the final velocity

Using equation of motion

`v_(f)^2=u^2+2as`

Put the value into the formula

`v_(f)^2=0+2*9.8*1.46`

`v_(f)=√(28.616)`

`v_(f)=5.34\ m/s`

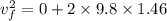
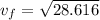
The velocity is 5.34 m/s downward.

We need to calculate the direction

Using formula of direction

`\tan\theta=(v_(y))/(v_(x))`

`\theta=\tan^(-1)((5.34)/(1.46))`

`\theta=74.7^(\circ)`

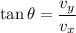
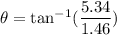
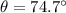
Hence, (a). The horizontal velocity is 1.46 m/s.

(b). The direction of the mug's velocity just before it hit the floor is 74.7° below the horizontal.