The correct question is:
Find the area of the surface generated by revolving about the x-axis, the portion of the astroid

Answer: The Surface Area is

Explanation:
First, we rewrite the expression in terms of x, because we are revolving about the x-axis, we want to integrate in terms of x. Doing that, we have
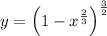
Next, we differentiate y with respect to x
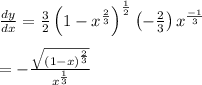
Thus,
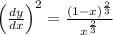
and so
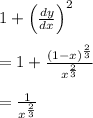
Therefore, the Surface Area is given as:
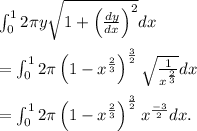
If we let
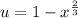
then
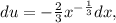
so we see that
