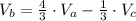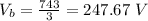Question

The potential at location A is 382 V. A positively charged particle is released there from rest and arrives at location B with a speed vB. The potential at location C is 785 V, and when released from rest from this spot, the particle arrives at B with twice the speed it previously had, or 2vB. Find the potential at B.

Answer 1

Answer: 247.67 V

Step-by-step explanation:

Given

Potential At A
`V_a=382\ V`

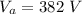
Potential at
`V_c=785\ V`

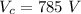
when particle starts from A it reaches with velocity
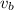`v_b` at Point while when it starts from C it reaches at point B with velocity
`2v_b`

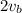
Suppose m is the mass of Particle

Change in Kinetic Energy of particle moving under the Potential From A to B

`q\cdot \left ( V_a-V_b\right )=0.5m\cdot (v_b)^2----1`

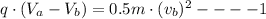
Change in Kinetic Energy of particle moving under the Potential From C to B

`q\cdot \left ( V_c-V_b\right )=0.5m\cdot (2v_b)^2-----2`

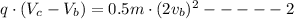
Divide 1 and 2 we get

`(V_a-V_b)/(V_c-V_b)=(v_b^2)/(4v_b^2)`

on solving we get

`V_b=(4)/(3)\cdot V_a-(1)/(3)\cdot V_c`

`V_b=(743)/(3)=247.67\ V`