Question

Which of the following points is a solution to the system of equations x - y = 1 and -x + 3y = - 7?

(-2,2) is a solution.
0 (-2, - 3) is a solution.
(1. - 2) is a solution.
(4.3) is a solution

Answer 1

(-2,-3)

Explanation:

Put the equations over each other.

`\binom{x - y = 1}{ - x + 3y = - 7 }`

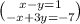
Subtract the x values.

`\binom{ - y = 1}{3y = - 7}`

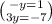
Subtract on both sides.

`2y = - 6`

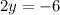
Divide on both sides.

`y = - 3`

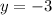
Insert the y value into one of the equations.

`x - ( - 3) = 1`

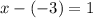
Get rid of the parenthesis.

`x + 3 = 1`

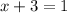
Subtract on both sides.

`x = - 2`

You could also individually plug in each solution into both equations to see if they are true.