Question

Which expression is equivalent to the following complex fraction?

StartFraction 2 Over x EndFraction minus StartFraction 4 Over y EndFraction divided by StartFraction negative 5 Over y EndFraction + StartFraction 3 Over x EndFraction

Answer 1

B on edge

i just finished it

Answer 2

Option b:
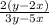`(2(y-2 x))/(3 y-5 x)` is the expression which is equivalent to
`((2)/(x)-(4)/(y))/((-5)/(y)+(3)/(x))`

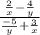
Step-by-step explanation:

The expression is
`((2)/(x)-(4)/(y))/(-(5)/(y)+(3)/(x))`

To solve the expression, let us take LCM in both numerator and denominator.

Thus, we have,

`(\left((2 y-4 x)/(x y)\right))/(\left((3 y-5 x)/(x y)\right))`

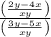
Dividing both fractions, we have,

`(2y-4x)/( 3y-5x)`

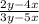
From numerator, let us take the common term 2 out,

`(2(y-2 x))/(3 y-5 x)`

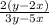
Thus, the expression equivalent to
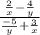`((2)/(x)-(4)/(y))/((-5)/(y)+(3)/(x))` is
`(2(y-2 x))/(3 y-5 x)`

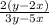
Hence, Option b is the correct answer.