Answer:
Part A)
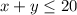
Part B) The solution in the attached figure
Explanation:
The complete question is
Suppose Rick has 40 ft of fencing with which he can build a rectangular garden. Let X represent the length of the garden and let Y represent the width.
A. Please write an inequality representing the fact that the total perimeter of the garden is at most 40 ft.
B. Please sketch part of the solution set for this inequality that represents all possible values for the length and width of the garden.
Part A)
Let
x ----> the length of the rectangular garden
y ----> the width of the rectangular garden
we know that
The perimeter of the rectangular garden is equal to
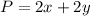
In this problem the word "at most" means "less than or equal to"
so
The inequality that represent this situation is
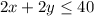
Simplify
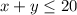
Part B) we have
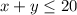
Isolate the variable y
subtract x both sides
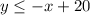
The solution of the inequality is the shaded area below the solid line
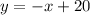
The slope of the solid line is negative (m=-1)
The y-intercept of the solid line is (0,20)
The x-intercept of the solid line is (20,0)
therefore
The solution is the triangular shaded area
see the attached figure
Remember that
Both the length and the width must be positive