A geometric sequence has a common ratio.
The formula for the nth term is
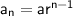
where,
- an = nth term of the sequence,
- a = first term of the sequence and
- r = common ratio
Given -
- A geometric sequence 2, -4, 8, ...
To find -
- the 12th term of the given geometric sequence
Solution -
A.T.Q, a = 2 and r = -2
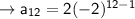
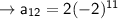
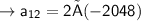

Hence, the 12th term is -4096.