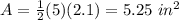Question

A triangle with 2 40 degree angles that surround a 5 inch side

Answer 1

The drawing in the attached figure

see the explanation

Explanation:

we know that

An isosceles triangle has two equal sides and two equal interior angles

In this problem

we have an isosceles triangle (because has two equal interior angles)

see the attached figure to better understand the problem

step 1

Find the length side AB

In the right triangle ABD

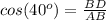`cos(40^o)=(BD)/(AB)` ----> by CAH (adjacent side divided by the hypotenuse)

we have

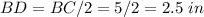`BD=BC/2=5/2=2.5\ in` ---> because is an isosceles triangle (the height bisect the base)

substitute

`cos(40^o)=(2.5)/(AB)`

`AB=(2.5)/(cos(40^o))=3.3\ in`

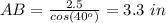
Find the length side AC

we know that

AC=AB ----> by definition of isosceles triangle

so

`AB=3.3\ in`

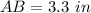
step 2

Find the perimeter

`P=AB+BC+AC`

`P=3.3+5+3.3=11.6\ in`

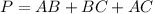
step 3

Find the height AD

In the right triangle ABD

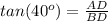`tan(40^o)=(AD)/(BD)` ----> by TOA (opposite side divided by the adjacent side)

`AD=tan(40^o)BD`

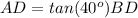
substitute the given values

`AD=tan(40^o)(2.5)=2.1\ in`

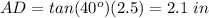
Find the area of triangle

`A=(1)/(2)(BC)(AD)`

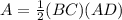
substitute

`A=(1)/(2)(5)(2.1)=5.25\ in^2`