Answer: The length of copper wire that can be produced is 40.2 m
Step-by-step explanation:
We are given:
Mass of chalcocite = 5.23 lb = 2374.42 g (Conversion factor: 1 lb = 454 g)
79.8 % (m/m) of copper
This means that 79.8 grams of copper is present in 100 grams of chalcocite
Applying unitary method:
In 100 grams of chalcocite, the mass of copper present is 79.8 grams
So, in 2374.42 grams of chalcocite, the mass of copper present will be =
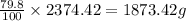
To calculate volume of a substance, we use the equation:
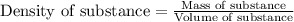
Density of copper =
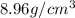
Mass of copper = 1873.42 g
Putting values in above equation, we get:
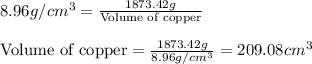
To calculate the length of the wire, we use the equation:
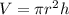
where,
V = volume of copper wire =
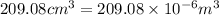 (Conversion factor:
(Conversion factor:
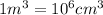 )
)
r = radius of the copper wire =
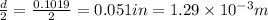 (Conversion factor: 1 in = 0.0254 m)
(Conversion factor: 1 in = 0.0254 m)
h = length/ height of the copper wire = ?
Putting values in above equation, we get:

Hence, the length of copper wire that can be produced is 40.2 m