Question

Chalcocite is a mineral that contains 79.8% of copper. How many meter of wire with diameter of 0.1019 in can be produced from 5.23 lb of chalcocite?

Vcylinder = π*r2h, density of copper is 8.96 g/cm3, 1 lb=454 g

102 m

40.2 m

10.1 m

2.59 × 104

211 m

Answer 1

Answer: The length of copper wire that can be produced is 40.2 m

Step-by-step explanation:

We are given:

Mass of chalcocite = 5.23 lb = 2374.42 g (Conversion factor: 1 lb = 454 g)

79.8 % (m/m) of copper

This means that 79.8 grams of copper is present in 100 grams of chalcocite

Applying unitary method:

In 100 grams of chalcocite, the mass of copper present is 79.8 grams

So, in 2374.42 grams of chalcocite, the mass of copper present will be =
`(79.8)/(100)* 2374.42=1873.42g`

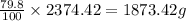
To calculate volume of a substance, we use the equation:

`\text{Density of substance}=\frac{\text{Mass of substance}}{\text{Volume of substance}}`

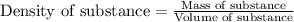
Density of copper =
`8.96g/cm^3`

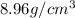
Mass of copper = 1873.42 g

Putting values in above equation, we get:

`8.96g/cm^3=\frac{1873.42g}{\text{Volume of copper}}\\\\\text{Volume of copper}=(1873.42g)/(8.96g/cm^3)=209.08cm^3`

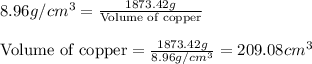
To calculate the length of the wire, we use the equation:

`V=\pi r^2h`

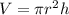
where,

V = volume of copper wire =
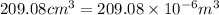`209.08cm^3=209.08* 10^(-6)m^3` (Conversion factor:
`1m^3=10^6cm^3` )

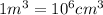r = radius of the copper wire =
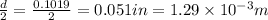`(d)/(2)=(0.1019)/(2)=0.051in=1.29* 10^(-3)m` (Conversion factor: 1 in = 0.0254 m)

h = length/ height of the copper wire = ?

Putting values in above equation, we get:

`209.08* 10^(-6)m^3=(3.14)* (1.29* 10^(-3))^2* h\\\\h=(209.08* 10^(-6))/(3.14* (1.29* 10^(-3))^2)=40.2m`

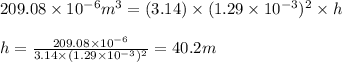
Hence, the length of copper wire that can be produced is 40.2 m