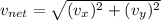Question

Firemen are shooting a stream of water at a burning buildingusing a high-pressure hose that shoots out the water with a speedof 25.0 m/s. as it leaves the end of the hose. Once it leaves thehose, the water moves in projectile motion. The firemen adjust theangle of elevation α of the hose until the water takes3.00 s to reach the building 45.0 m away. You can ignore airresistance; assume that the end of the hose is at grounglevel.

a) Find the angle of elevation αb) Find the speed and acceleration of the water at the highestpoint in its trajectoryc) How high above the ground does the water strike thebuilding, and how fast is it moving just before it hits thebuilding?

Answer 1

Step-by-step explanation:

Given

Firemen shoot the water stream at an angle of \alpha

launch speed
`u=25\ m/s`

it takes it
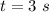`t=3\ s` to reach the building

Building is
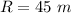`R=45\ m` from launch point

Considering horizontal motion

`R=u\cos \alpha \cdot t`

`45=25\cos \alpha \cdot 3`

`\cos \alpha =0.6`

`\alpha =53.13^(\circ)`

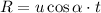
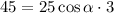
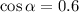
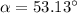
(b)At highest point vertical velocity becomes zero and there is only horizontal velocity

`velocity=u\cos \alpha`

`velocity=25\cdot \cos \53.13`

`velocity=15\ m/s`

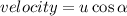
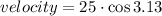
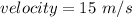
net acceleration will be acceleration due to gravity which will be acting downward

(c)height reached by water stream is given by

`y=ut+(1)/(2)at^2`

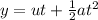
where,

y=displacement

u=initial velocity in vertical direction

a=acceleration

t=time

net velocity at this instant is the vector sum of vertical and horizontal velocity

vertical velocity
`v_y=u\sin \alpha -g\cdot t`

`v_y=25\sin (53.13)-9.8\cdot 3`

`v_y=-9.4\ m/s`

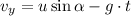
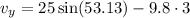
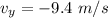
Horizontal velocity
`v_x=u\cos \alpha =25\cos (53.13)`

`v_x=15`

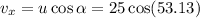
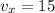
net velocity
`v_(net)=√((v_x)^2+(v_y)^2)`

`v_(net)=√(313.36)=17.70\ m/s`