Answer:
0.5 is the probability that the student chooses both math and Spanish.
Explanation:
We are given the following in the question:
M: Math class
S: Spanish class
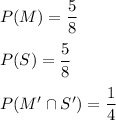
We have to evaluate the probability that she chooses both math and Spanish.
According to De-Morgans law
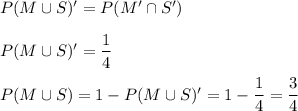
Now, using the relation:

Thus, 0.5 is the probability that the student chooses both math and Spanish.