Question

A pitot tube indicates a pressure of 155 kPa when placed in an air stream in which the temperature is 15°C and the Mach number is 0.7. Find the static pressure in the flow. Also, find the stagnation temperature in the flow.

Answer 1

To solve this problem we will start by defining the relationship of the pitot tube and the value indicated in the pressure. We will take advantage of this relationship to obtain a ratio between the defined pressures and proceed to calculate the total and static pressure of the system through the correlation of pressure in isotropic systems. Finally we will perform this same procedure for pressure. Pitot tube measure the total pressure minus static pressure, then

`p_0 - p = 155kPa`

`(p_0)/(p) -1 = (155)/(p)`

`(p_0)/(p) = (155)/(p) +1`

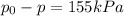
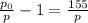
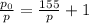
Express the total pressure and static pressure ratio

`(p_0)/(p) = [1+(\gamma-1)/(2)M^2]^{(\gamma)/(\gamma-1)}`

`(155)/(p) +1 = [1+(1.4-1)/(2)(0.7)^2]^{(1.4)/(1.4-1)}`

`(155)/(p) +1=1.3871`

`p = 400.4kPa`

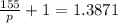
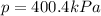
Hence the static pressure is 400.4kPa

Express stagnation to static temperature ratio,

`(T_0)/(T) = 1+(\gamma-1)/(2)M^2`

`(T_0)/((15+273)K) = 1+(1.4-1)/(2)(0.7)^2`

`T_0 = 316.224K`

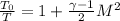
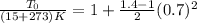
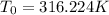
Therefore the stagnation temperature is 316.224K