Answer: A.8488
Explanation:
Poisson distribution formula :
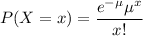
, where
 = mean of the distribution.
= mean of the distribution.
Let x be the random variable that represents the number of defects.
Given : The average number of defects per standard sheet of steel is 2.
For 3 sheets , the average number of defects per standard sheet of steel = 2 x 3 = 6
i.e.
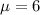
Now , the probability that the first three units manufactured in this batch will contain at least a total of 4 defects will be :-

Hence, the probability that the first three units manufactured in this batch will contain at least a total of 4 defects will be 0.8488.
Thus , the correct option is A .8488.