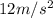Question

A car increases its forward velocity uniformly from 40 m/s to 80 m/s while traveling a distance of 200 m. What is its acceleration during this time?

Answer 1

To solve this problem we will apply the linear motion kinematic equations. For this purpose we know that the squared change of the initial velocity and the final velocity is equal to twice the acceleration by the distance traveled. Mathematically this can be expressed as,

`v_f^2 - v_i^2 =2ax`

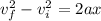
Where,

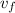`v_f` = Final velocity

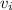`v_i` = Initial velocity

`a` = Acceleration

`x` = Displacement

Replacing,

`(80)^2 - (40)^2= 2a(200)`

`a = ((80)^2 - (40)^2)/(2(200))`

`a = 12m/s^2`

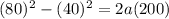
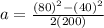
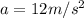
Therefore the acceleration during this time is
`12m/s^2`