Question

A company wants to determine the amount of a vitamin mix that can be enclosed in a capsule like the one shown. The capsule has a radius of 3millimeters (mm) and a length of 10 mm. How much vitamin mix is needed?

Answer 1

226.285 mm³ vitamin mix is needed

Solution:

Radius of the capsule = 3 mm

Volume of the hemisphere =
`(2)/(3) \pi r^(3)`

`$\begin{aligned}&=(2)/(3) \pi * 3^(3)\\&=18 \pi\end{aligned}`

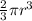
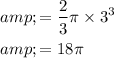
Volume of the hemisphere = 18π

Volume of the 2 hemisphere = 2 × 18π = 36π

Radius of the cylinder = 3 mm

Height of the cylinder = 10 – 3 – 3 = 4 mm

Volume of the cylinder =
`$\pi r^(2) h`

`$\begin{aligned}&=\pi * 3^(2) * 4\\&=36 \pi\end{aligned}`

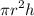
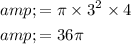
Volume of the cylinder = 36π

Volume of the capsule = volume of the 2 hemisphere + volume of the cylinder

= 36π + 36π

= 72π

`$=72 * (22)/(7)`

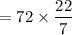
= 226.285 mm³

Volume of the capsule = 226.285 mm³

Hence 226.285 mm³ vitamin mix is needed.