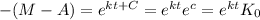Question

In the theory of learning, the rate at which a subject is memorized is assumed to be proportional to the amount that is left to be memorized. Suppose M denotes the total amount of a subject to be memorized and A(t) is the amount memorized in time t > 0. Determine a differential equation for the amount A(t). (Assume the constant of proportionality is k > 0. Use A for A(t)

Answer 1

`(dA)/(dt) \propto M-A`

`(dA)/(dt)= k (M-A)`

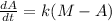
And the solution for this equation is:

`(dA)/(M-A) = k dt`

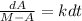
Using the substitution u = M-A, we have that du = -dA and after integrate we got:

`-ln |M-A|= kt +C`

C is a constant.

Now we can apply exponential in both sides and we got:

`-(M-A)= e^(kt +C)= e^(kt) e^c = e^(kt) K_0`

`A-M = K_0 e^(kt)`

`A(t) = M+ K_0 e^(kt)`

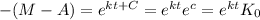
Explanation:

Let's define some notation first :

`M` represent the total amount of the subject to be memorized

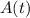`A(t)` represent the amount memorized at time t

t represent the time

k is a constant of proportionality

For this case we know that the rate of memorizing is proportional to the amount left to be memorized.

So then we can create the following relationship:

`(dA)/(dt) \propto M-A`

`(dA)/(dt)= k (M-A)`

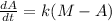
Where k>0. We can solve this differential equation like this:

`(dA)/(M-A) = k dt`

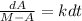
Using the substitution u = M-A, we have that du = -dA and after integrate we got:

`-ln |M-A|= kt +C`

C is a constant.

Now we can apply exponential in both sides and we got:

`-(M-A)= e^(kt +C)= e^(kt) e^c = e^(kt) K_0`

`A-M = K_0 e^(kt)`

`A(t) = M+ K_0 e^(kt)`