Question

In a semiconductor company's quality control test, a machine found that 11 out of a sample of 355 computer chips were defective. How many of the 3596 such chips that the company makes each month would you expect to be defective?

Answer 1

I would expect 111.48 of the chips that the company makes each month to be defective.

Explanation:

For each computer chips, there are only two possible outcomes. Either they are defective, or they are not. So we use the binomial probability distribution to solve this problem.

Binomial probability distribution

Probability of exactly x sucesses on n repeated trials, with p probability.

The expected value of the binomial distribution is:

`E(X) = np`

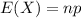
In a semiconductor company's quality control test, a machine found that 11 out of a sample of 355 computer chips were defective.

This means that
`p = (11)/(355) = 0.0310`

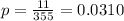
How many of the 3596 such chips that the company makes each month would you expect to be defective?

Thi is E when
`n = 3596`

`E(X) = np = 3596*0.0310 = 111.48`

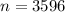
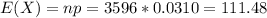
I would expect 111.48 of the chips that the company makes each month to be defective.