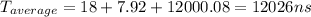Question

A computer has a cache and main memory. 20 ns are required to reference a word that is in the cache. If the word is in main memory but not in the cache, 60 ns are needed to load it into the cache (this includes the time to originally check the cache), and then the reference is started again. If the word is not in main memory, 10 ms are required to fetch the word from disk, followed by 60 ns to copy it to the cache, and then the reference is started again. The cache hit ratio is 0.9 and the main memory hit ratio is 0.99. What is the average time in ns required to access a referenced word on this system?

Answer 1

`T_(average) =12026ns`

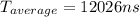
Step-by-step explanation:

Given Information:

`T_(cache)=20 ns`

`T_(main)=60ns`

`T_(disk) =12ms=12,000,000ns`

`hit_(cache) =0.9`

`miss_(cache) =1-0.9=0.10`

`hit_(main) =0.99`

`miss_(main) =1-0.99=0.01`

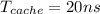
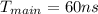
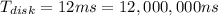
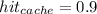
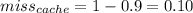
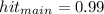
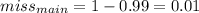
There are 3 possible cases

1. Location of reference word is in cache

`T_(cache)*hit_(cache) =20*0.9=18ns`

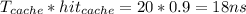
2. Location of reference word is not in cache but in main memory

`(T_(cache)+T_(main))*(miss_(cache)*hit_(main)) =(20+60)*(0.10*0.99)=7.92ns`

3. Location of reference word is neither in cache nor in main memory

`(T_(cache)+T_(main)+T_(disk))*(miss_(cache)*miss_(main))`

`(20+60+12,000,000)*(0.10*0.01)=12000.08 ns`

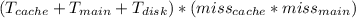
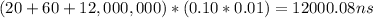
The average time required to access a referenced word on this system is simply the sum of above 3 cases

`T_(average) =18+7.92+12000.08=12026ns`