Answer:
D) 11/3
Explanation:
Let x represent monthly salary.
We have been given that for each month of a given year except December, a worker earned the same monthly salary and donated one-tenth of that salary to charity.
Salary earned in 11 months would be
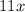 .
.
Money donated in 11 months would be
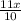 .
.
Further we are told that in December, the worker earned N times his usual monthly salary and donated one-fifth of his earnings to charity.
Salary for December would be
 .
.
Money donated in December would be
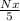 .
.
The worker's charitable contributions totaled one-eighth of his earnings for the entire year that is
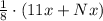 .
.
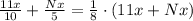
Dividing whole equation by x, we will get:
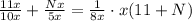
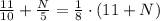
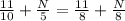
Combine like terms:
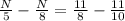

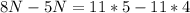
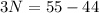
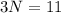
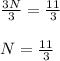
Therefore, the value of N is 11/3 and option D is the correct choice.