Part A: The equation of the ship's path is
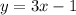
Part B: The two ships sails perpendicular to each other.
Step-by-step explanation:
Part A: It is given that
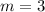 and point (2, 5)
and point (2, 5)
Substituting these in the slope intercept form, we have,
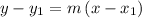
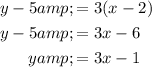
Thus, the equation of the ship's path in slope intercept form is
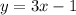
Part B: The equation of the second ship is
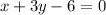
Let us bring the equation in the form of slope intercept form.
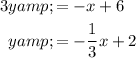
Thus, from the above equation the slope is
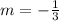
To determine the two ships sailing perpendicular to each other, we have

where
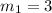 and
and
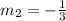
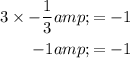
Since, both sides of the equation are equal, these two ships sails perpendicular to each other.