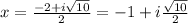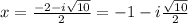Answer:
The roots are
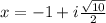
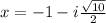
Explanation:
we have
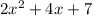
To find the roots equate the equation to zero
so
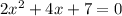
we know that
The formula to solve a quadratic equation of the form
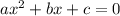
is equal to
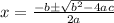
in this problem we have
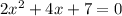
so
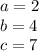
substitute in the formula
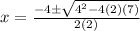
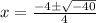
Remember that
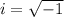
so
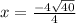
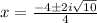
simplify
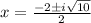
therefore
The roots are