Question

Assume that the random variable X is normally​ distributed, with mean

μ=50 and standard deviation σ=8. Compute the probability. Be sure to draw a normal curve with the area corresponding to the probability shaded.
P(X ≤ 45)

Answer 1

P(X ≤ 45)=0.2643

Explanation:

We were given that the random variable X is normally​ distributed, with mean

μ=50 and standard deviation σ=8.

We want to compute the probability, P(X ≤ 45).

First, we need to calculate the z-score of X=45 using

`Z=(X-\mu)/(\sigma)`

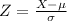
We substitute these values to get:

`Z=(45-50)/(8)`

`Z=(-5)/(8) =-0.63`

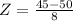
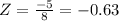
We now read area that corresponds to -0.63 in the standard normal distribution table.

This gives us P(X ≤ 45)=0.2643