Answer:
0.118 is the probability someone will spend no more than 30 minutes reading online national news reports.
Explanation:
We are given the following information in the question:
Mean, μ = 49 minutes
Standard Deviation, σ = 16 minutes
We are given that the distribution of time an individual reads is a bell shaped distribution that is a normal distribution.
Formula:
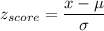
P(no more than 30 minutes)
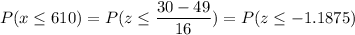
Calculation the value from standard normal z table, we have,
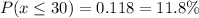
0.118 is the probability someone will spend no more than 30 minutes reading online national news reports.