Answer:
1. 0.4452; 2. 0.0548; 3. 0.0545; 4. 0.7254; 5. Time is about 5.68 minutes or more.
Explanation:
We have a normal distribution with known parameters, that is, for the population mean and for the population standard deviation:

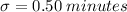
For each of the questions, we have to transform either raw score to a z-score as a way to use the cumulative standard normal distribution table for consulting the probabilities values for each z-score.
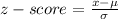
We also need to have into account that the normal distribution is symmetrical, an indispensable property to calculate negative z-scores, that is, values below the population mean.
1. The probability that calls last between 4.8 and 5.6 minutes
The corresponding z-scores for 4.8 minutes and 5.6 minutes are respectively:

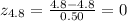
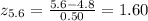
As we can see, the z-score for a raw value of 4.8 coincides with the population mean, thus the z-score = 0. The probability between 4.8 and 5.6 minutes is the resulting difference between these two values. As a result, consulting the associated probability for each z-score in the cumulative standard normal table, we have:
For z = 0, P(z<0) = 0.50000.
For z = 1.60, P(z<1.60) = 0.94520
So, the probability that calls last between 4.8 and 5.6 minutes is:
P(4.8<x<5.6) = (z<1.60) - P(z<0) = 0.94520 - 0.50000 = 0.44520 = 0.4452 (four decimal places).
2. The probability that calls last more than 5.6 minutes
We already know from previous answer that the cumulative probability for a raw score = 5.6 minutes (that corresponds to a z-score = 1.60) is P(z<1.60) = 0.94520.
Thus, the probability for call that last more than 5.6 minutes is:
P(x>5.6) = P(z>1.60) = 1 - P(z<1.60) = 1 - 0.94520 = 0.0548 (four decimal places).
3. The probability that calls last between 5.6 and 6.5 minutes
We know the probability for 5.6 minutes from former answers (P(z<1.60) = 0.94520. We still need to consult the probability for 6.5 minutes, following the same procedure:

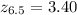
This corresponds with a cumulative probability of P(z<3.40) = 0.99966.
So, the probability that calls last between 5.6 and 6.5 minutes is:
P(5.6<x<6.5) = P(z<3.40) - P(z<1.60) = 0.99966 - 0.94520 = 0.05446 or 0.0545 (rounding to four decimal places).
4. The probability that calls last between 4.5 and 6.5 minutes
We already know that probability for P(x<6.5) = P(z<3.40) = 0.99966.
For the probability of P(x<4.5), we can see that the value is slightly below the population mean (x = 4.8 minutes). The z-score is:
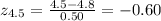
Since we have a negative value and the cumulative standard normal table only permits us consult positive values, that is, z = 0.60, we can find the probability for this z-score, and then subtract it from 1 to find the corresponding value for P(z<-0.60). Then
P(z<0.60) = 0.72575; P(z<-0.60) = 1 - P(z<0.60) = 1 - 0.72575 = 0.27425.
The probability that calls last between 4.5 and 6.5 minutes is:
P(4.5<x<6.5) = P(-0.60<z<3.40) = 0.99966 - 0.27425 = 0.72541 or 0.7254.
5. The length of the longest (in duration) 4 percent of the calls. What is this time?
In the cumulative standard normal table, we can consult the 1 - 0.04 = 0.96 probability that corresponds to a z-score. The value for z is approximately z = 1.75. Then, using the formula for z-scores:

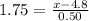
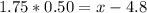
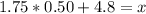
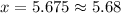
Then, the length of the longest (in duration) 4 percent of the calls is about 5.68 minutes or more.
The corresponding graphs can be seen below.