Question

Price deregulation in the airline industry has promoted competition and a variety of fare structures. Prior to deciding on a price change, a particular airline is interested in obtaining an estimate of the proportion of the market that it presently captures for a certain region. A random sample of 300 passengers indicatesthat 80 used that airline.

a. Find a point estimate ofthe proportion ofthe market that usesthis particular airline.
b. Find a 95% confidence interval for the proportion that uses this airline. (c) Can the airline conclude that its market share is more than 25%

Answer 1

a) 0.2667

b) (0.2167,0.3167)

c) We cannot conclude that its market share is more than 25%.

Explanation:

We are given the following in the question:

Sample size, n = 300

Number of passengers who used airlines, x = 80

a) point estimate of the proportion of the market that uses this particular airline.

`\hat{p} = (x)/(n) = (80)/(300) = $$0.2667`

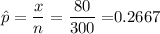
b) 95% confidence interval

`\hat{p}\pm z_(stat)\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`

`z_(critical)\text{ at}~\alpha_(0.05) = \pm 1.96`

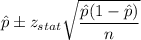
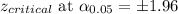
Putting the values, we get:

`0.2667 \pm 1.96(\sqrt{(0.2667(1-0.2667))/(300)}) = 0.2667 \pm 0.0500\\\\=(0.2167,0.3167)`

c) First, we design the null and the alternate hypothesis

`H_(0): p = 0.25\\H_A: p > 0.25`

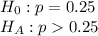
Formula:

`\hat{p} = (x)/(n) = (52)/(400) = 0.13`

`z = \frac{\hat{p}-p}{\sqrt{(p(1-p))/(n)}}`

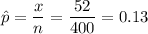
Putting the values, we get,

`z = \displaystyle\frac{0.2667-0.25}{\sqrt{(0.25(1-0.25))/(300)}} = 0.6664`

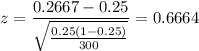
Now, we calculate the p-value from the table.

P-value = 0.252

Since the p-value is greater than the significance level, we fail to reject the null hypothesis and accept it.

Thus, we cannot conclude that its market share is more than 25%.