Answer : The concentration of
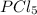 and
and
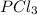 at equilibrium is, 0.0031 M and 0.0741 M respectively.
at equilibrium is, 0.0031 M and 0.0741 M respectively.
Explanation : Given,
Moles of
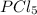 = 0.166 mol
= 0.166 mol
Volume of solution = 2.15 L
First we have to calculate the concentration of
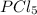
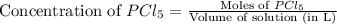
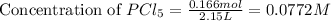
Now we have to calculate the concentration of
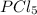 and
and
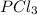 at equilibrium.
at equilibrium.
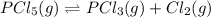
Initial conc. 0.0772 0 0
At eqm. 0.0772-x x x
The expression for equilibrium constant is:
![K_c=([PCl_3][Cl_2])/([PCl_5])](https://img.qammunity.org/2021/formulas/chemistry/high-school/7kc3ykrhi4n2wnacy2qx27jjvxou8mgh41.png)
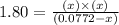
By solving the term, we get the value of 'x'.
x = 0.0741
Thus,
The concentration of
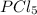 at equilibrium = (0.0772-x) = (0.0772-0.0741) = 0.0031 M
at equilibrium = (0.0772-x) = (0.0772-0.0741) = 0.0031 M
The concentration of
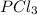 at equilibrium = x = 0.0741 M
at equilibrium = x = 0.0741 M