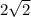Question

In the right triangle shown, AC = BCAC=BCA, C, equals, B, C and AB = 4\sqrt{2}AB=4 2 ​ A, B, equals, 4, square root of, 2, end square root. How long are each of the legs? Answer exactly, using a radical if needed.

Answer 1

The answer is 4 !

Step-by-step explanation:

I got it wrong and just started guessing till i got it right.

Answer 2

The length of the legs AC and BC are 2√2

Step-by-step explanation:

It is given that the sides AC = BC and AB = 4√2

Now, we shall find the lengths of the sides AC and BC.

Let the length of the sides AC and BC be x.

The image of the triangle having these measurements is attached below:

Using Pythagoras theorem, we shall determine the value of x.

`AB^(2) =AC^(2) +CB^(2)`

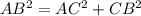
Substituting the values, we have,

`(4√(2) )^(2) =x^(2) +x^(2)`

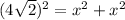
Simplifying, we have,

`8*2=2x^(2)`

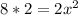
Dividing both sides by 2, we have,

`8=x^(2)`

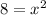
Taking square root on both sides, we get,

`2√(2) =x`

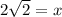
Thus, the lengths of AC and BC is
`2√(2)`