Answer:
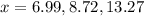 .
.
Explanation:
We have been given an equation
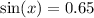 . We are asked to solve the given equation in the interval
. We are asked to solve the given equation in the interval
![[(3\pi)/(2),(9\pi)/(2)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/jlmzjg654au6rhiomxwgreln5rueahv09q.png) .
.
Taking inverse of sine function, we will get:
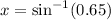
General solutions of the equation would be:
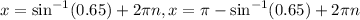
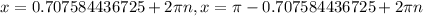
Now, we need to find value of x such that:
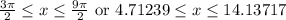
When
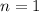
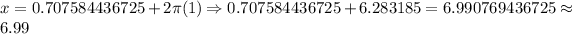
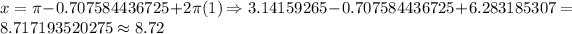
When
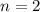 :
:
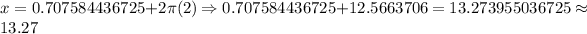

We can see that
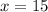 is greater than
is greater than
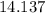 , therefore, the solutions for the given equation are
, therefore, the solutions for the given equation are
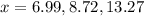 .
.